Peluang suatu kejadian A sama dengan jumlah terjadinya kejadian A dibagi dengan seluruh yang mungkin.
P(A) = k / n
Dimana
k : jumlah terjadinya kejadian A
n : jumlah seluruh yang mungkin
Jika kita melakukan percobaan, maka himpunan semua hasil disebut Ruang Sampel
Contoh:
1. Percobaan melempar uang logam 3 kali.
A adalah kejadian muncul tepat dua muka berturut-turut.
Maka :
S = {mmm,mmb,mbm,mbb, bmm, bmb, bbm, bbb}
A = {mmb, bmm}
n(S) = 23 = 8
n(A) = 2
P(A) = 2/8 = 1/4
2. Percobaan melempar dadu satu kali.
A adalah kejadian muncul sisi dengan mata dadu genap.
Maka :
S = {1,2,3,4,5,6}
A = {2,4,6}
n(S) = 6
n(A) = 3
P(A) = 3/6 = 1/2
Jika peluang terjadinya A adalah P(A) dan peluang tidak terjadinya A adalah P(A) maka berlaku
_
P(A) + P(A) = 1
Contoh:
Dari setumpuk kartu Bridge yang terdiri dari 52 kartu diambil 1 kartu. Berapakah peluang kartu yang terambil bukan kartu King?
Jawab:
P (King) = 4/52 = 1/13
P bukan King = 1 - 1/13 = 12/13
PELUANG KEJADIAN BEBAS DAN TAK BEBAS
DEFINISI Dua kejadian A dan B dikatakan bebas jika dan hanya jika
P(AÇB) = P(A). P(B)
Contoh:
Dalam tas I terdapat 4 bola putih dan 2 bola hitam. Dalam tas II terdapat 3 bola putih dan 5 bola hitam.
Sebuah bola diambil dari masing-masing tas.
a) Keduanya berwarna putih
b) Keduanya berwama hitam
Jawab:
Misal
A = bola putih dari tas I
B = bola putih dari tas II
P(A) = 4/6
P(B) = 3/8
_ _
P(A) = 2/6 P(B) = 5/8
a. P(AÇB) = P (A) . P (B) = 4/6 . 3/8 = 1/4
_ _ _ _
b. P((A) Ç P(B)) = P(A). P(B) = 2/6 . 5/8 = 5/24
DEFINISI
Jika A dan B dua kejadian yang saling asing maka berlaku :
P (AUB) = P(A) + P(B)
Contoh:
Pada pelemparan sebuah dada merah (m) dan sebuah dadu putih (p).
Maka: S={(1,1), (1,2), .....,(1,6), (2,1),(2,2),.....(6,6)}
n(S) - (6)2 = 36
A : Kejadian muncul m + p = 6 ® {(1,5) (2,4) (3,3) (4,2) (5,1)}
n(A) = 5
B : Kejadian muncul m + p = 10 ® {(4,6), (5,5), (6,4)}
n(B) = 3
P(A) = 5/36 P(B) = 3/36
AUB :Kejadian muncul m + p = 6 atau m + p = 10 ®
{ (1,5) (2,4) (3,3) (4,2) (4,6) (5,1) (5,5) (6,4) }
n(AUB) = 8
P(AUB) = 8/36 = P(A) + P(B)
A dan B kejadian yang saling asing.
DEFINISI
Jika A dan B dua kejadian yang tidak saling asing maka berlaku
P(AUB) = P(A) + P(B) - P(AÇB)
Contoh:
Dalam pelemparan sebuah dada S : { 1, 2, 3, 4, 5, 6}
A : Kejadian muncul sisi dengan banyaknya mata dadu bilangan ganjil = { 1, 3, 5 } ® n(A) = 3/6
B : Kejadian muncul sisi dengan banyaknya mata dadu bilangan prima = {2, 3, 5} ® n(B) = 3/6
P(AUB) = 4/6 = P(A) + P(B)
A dan B kejadian yang tidak saling asing.


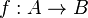




 dengan a1 tidak sama dengan a2 berlaku f(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2f(a1) sama dengan f(a2).
dengan a1 tidak sama dengan a2 berlaku f(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2f(a1) sama dengan f(a2).